Specific Capacity Calculator
Specific Capacity Calculator
This calculator estimates aquifer transmissivity using the specific capacity method presented by Bradbury and Rothschild, 1985. This method is best suited for estimating aquifer transmissivity in situations where a single time and drawdown measurement is available. Such data is commonly included in many well installation logs, where a proper pumping test has not been performed. This may be the only method of estimating aquifer transmissivity in such a situation.
Mathematical Development
Specific capacity of a well is defined as the discharge rate per foot of drawdown (Q/s). Using the Jacob approximation to the Theis solution for unsteady flow in confined aquifers, Equation 1 shows specific capacity as a function of aquifer transmissivity. Because the specific capacity method is ultimately derived from the Theis solution, it incorporates all Theis assumptions (with the exception of full penetration of the aquifer by the well, as described below).
Equation 1
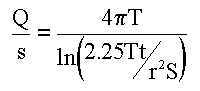
where:
Q = well discharge
s = drawdown in the well at time t
T = transmissivity of the aquifer
r = radial distance to the point the drawdown is measured
S = storativity of the aquifer
Q/s is defined as the specific capacity of a well, or the volume of water available per unit of drawdown.
To account for partial penetration, Sternberg (1973) described unsteady-state drawdown in a well with Equation 2:
Equation 2:
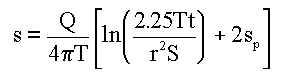
where sp is a partial penetration factor given by Brons and Marting (1961) as
Equation 3:
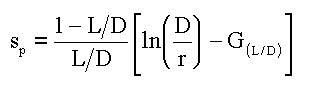
where:
D = Aquifer Thickness
L = Length of the Open Interval of the Borehole
G = a function of D and L, and is given by Equation 4
Equation 4:
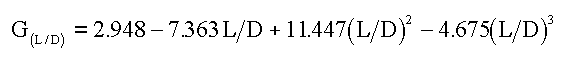
Equation 4 is a polynomial fitted to data by Brons and Marting by multiple regression with a correlation coefficient of 0.992.
As shown with Equation 5, Equation 2 can not be solved directly for transmissivity.
Equation 5:
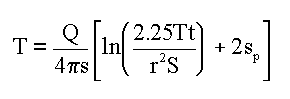
Infinite Extent uses an iterative approach similar to that presented by Bradbury and Rothschild, to solve for Transmissivity using Equation 5.
Comparison with Bradbury and Rothschild
Bradbury and Rothschild include example calculations where transmissivity is estimated for two wells. In comparison with Infinite Extent, the following results for transmissivity in square feet per second were obtained.
Well 1 Well 2
Bradbury and Rothschild 5.93317e-3 4.56944e-3
Infinite Extent 5.93291e-3 4.56705e-3
Estimating Storativity:
To use this method, an estimate of storativity is required when the well data is entered.
Typical storativity values are:
0.0002 for confined aquifer
0.002 for leaky aquifer
0.2 for unconfined aquifer
Full penetration is assumed if aquifer thickness or open interval is not entered. Full penetration is also assumed if the open interval is larger in magnitude than aquifer thickness.
Accuracy:
Based on Starpoint Software research, the most important factor in the accuracy is an accurate estimate of the aquifer storativity. When storativity is known correctly, the specific capacity method is nearly as accurate as the Theis Type Curve method. Of course, storativity will rarely be known before the test. Also the test is usually limited to a few data points, and therefore the benefit of averaging across many measurements is lost.
This method is most commonly used when drawdown is measured in the pumping well, and therefore well loss is likely to affect the calculation results.
The specific capacity method should be used only when data limitations preclude any more detailed analysis.